Answer:
See proof below
Explanation:
On the left hand side we have
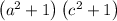
Apply the FOIL method to get

Simplify to get
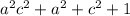
On the right hand side we have
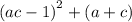
Expand
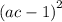
=
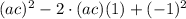
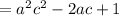 (1)
(1)
Expand
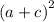
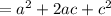 (2)
(2)
Add (1) and (2) to get the entire right side
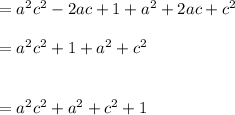 (by rearranging terms)
(by rearranging terms)
Looking at the left side and right side simplified expressions we see they are the same.
Hence proved