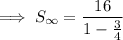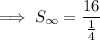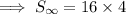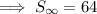Question

NO LINKS!! Please help me with this problem. Part 2ff​

Answer 1

R=12/16

Use formula s=a1/1-r

S=16/1-3/4

S=64

Answer 2

`S_(\infty)=64`

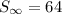
Explanation:

Given geometric series:

`16+12+9+(27)/(4)+...`

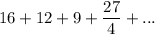
By inspection, the first term, a, is:

`\implies a=16`

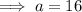
Find the common ratio, r, by dividing one term by the previous term:

`\implies r=(12)/(16)=(3)/(4)`

`\boxed{\begin{minipage}{5.5 cm}\underline{Sum of an infinite geometric series}\\\\$S_(\infty)=(a)/(1-r)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\ \phantom{ww}$\bullet$ $r$ is the common ratio.\\\end{minipage}}`

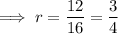
To find the sum of the infinite geometric series, substitute the found values of a and r into the formula:

`\implies S_(\infty)=(16)/(1-(3)/(4))`

`\implies S_(\infty)=(16)/((1)/(4))`

`\implies S_(\infty)=16 * 4`

`\implies S_(\infty)=64`