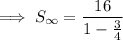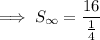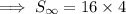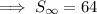Answer:
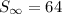
Explanation:
Given geometric series:

By inspection, the first term, a, is:
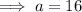
Find the common ratio, r, by dividing one term by the previous term:


To find the sum of the infinite geometric series, substitute the found values of a and r into the formula: