Question

For the polynomial g(x)=x^3−10x^2+25x−6, (a) identify the domain, range, and end behavior of the function, (b) apply the Rational Root Theorem, (c) apply Descartes' rule of signs, (d) use the remainder and factor theorems to factor the polynomial completely, (e) list all zeros, including complex zeros.

Answer 1

(a) Domain: (-∞ ,∞) Range: (-∞ ,∞)

`\textsf{As} \; x \rightarrow -\infty, \; f(x) \rightarrow - \infty`

`\textsf{As} \; x \rightarrow +\infty, \; f(x) \rightarrow + \infty`

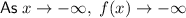
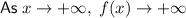
(b) x = 6

(c) See below.

(d) g(x) = (x - 6)(x² - 4x + 1)

(e) x = 6, x = 2 + √3, x = 2 - √3

Explanation:

Given polynomial:

`g(x)=x^3-10x^2+25x-6`

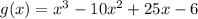
Part (a)

The domain of a function is the set of all possible input values (x-values).

The range of a function is the set of all possible output values (y-values).

Both the domain and range are unrestricted, therefore:

• Domain: (-∞ ,∞)
• Range: (-∞ ,∞)

As the leading coefficient is positive and the degree of the polynomial is odd, the end behavior of the function is:

• 
  `\textsf{As} \; x \rightarrow -\infty, \; f(x) \rightarrow - \infty`

• 
  `\textsf{As} \; x \rightarrow +\infty, \; f(x) \rightarrow + \infty`

Part (b)

Rational Root Theorem

`(p)/(q)=\frac{\textsf{a factor of the last term $(a_0)$}}{\textsf{a factor of the first term $(a_n)$}}`

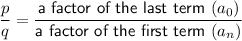
where:

`f(x)=a_n x^n+a_(n-1) x^(n-1) +... + a_2 x^2+a_1 x +a_0`

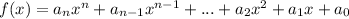
Identify the factors (both positive and negative) of the constant of the polynomial. The factors are the possible values of p:

• p = ± 1, ± 2, ± 3, ± 6

Identify the factors (both positive and negative) of the leading coefficient of the polynomial. These factors are the possible values of q.

• q = ± 1

Find each possible value of p/q

`\implies (p)/(q)=(\pm 1)/(\pm 1), (\pm 2)/(\pm 1), (\pm 3)/(\pm 1), (\pm 6)/(\pm 1)=\pm1, \pm2, \pm 3, \pm6`

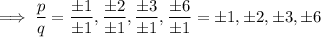
Therefore, the possible rational roots of g(x) are:

• ± 1, ± 2, ± 3, ± 6

Substitute each of the possible roots into g(x). Any root that results in f(x) = 0 is an actual rational root.

`x=-1 \implies g(-1)=(-1)^3-10(-1)^2+25(-1)-6=-42`

`x=1 \implies g(1)=(1)^3-10(1)^2+25(1)-6=10`

`x=-2 \implies g(-2)=(-2)^3-10(-2)^2+25(-2)-6=-104`

`x=2 \implies g(2)=(2)^3-10(2)^2+25(2)-6=12`

`x=-3 \implies g(-3)=(-3)^3-10(-3)^2+25(-3)-6=-198`

`x=3 \implies g(3)=(3)^3-10(3)^2+25(3)-6=6`

`x=-6 \implies g(-6)=(-6)^3-10(-6)^2+25(-6)-6=-732`

`x=6 \implies g(6)=(6)^3-10(6)^2+25(6)-6=0`

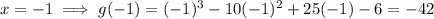
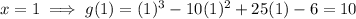
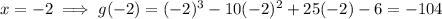
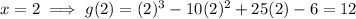
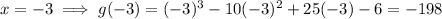
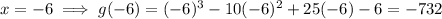
Therefore, the actual rational root is x = 6.

Part (c)

Descartes' Rule of Signs tells us the maximum number of positive and negative roots.

Positive root case

`g(x)=+x^3-10x^2+25x-6`

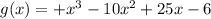
As there are 3 sign changes, the maximum possible number of positive roots is 3.

Negative root case

`\begin{aligned}g(-x)&=(-x)^3-10(-x)^2+25(-x)-6\\ &=-x^3-10x^2-25x-6 \end{aligned}`

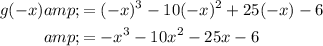
As there are no sign changes, there are no negative roots.

Part (d)

Remainder Theorem

When we divide a polynomial f(x) by (x − c) the remainder is f(c).

Factor Theorem

If f(x) is a polynomial, and f(a) = 0, then (x – a) is a factor of f(x).

From part (b) we know that f(6) = 0, so (x - 6) is a factor of g(x):

Use long division to find the other factor:

`\large \begin{array}{r}x^2-4x+1\phantom{)}\\x-6{\overline{\smash{\big)}\,x^3-10x^2+25x-6\phantom{)}}}\\{-~\phantom{(}\underline{(x^3-6x^2)\phantom{-b000000)}}\\-4x^2+25x-6\phantom{)}\\-~\phantom{()}\underline{(-4x^2+24x)\phantom{))..)}}\\x-6\phantom{)}\\-~\phantom{()}\underline{(x-6)\phantom{}}\\0 \phantom{)}\end{array}`

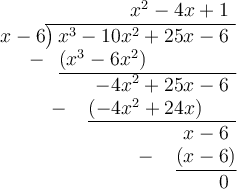
(x² - 4x + 1) cannot be factored further.

Therefore the factored polynomial is:

• 
  `g(x)=(x-6)(x^2-4x+1)`

Part (e)

The zeros of a polynomial are the values of x when f(x) = 0:

`\implies g(x)=0`

`\implies (x-6)(x^2-4x+1)=0`

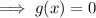
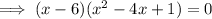
Therefore:

`\implies x-6=0`

`\implies x^2-4x+1=0`

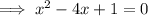
We have already established that x = 6 is a zero.

To find the other zeros, use the quadratic formula.

`\boxed{\begin{minipage}{3.6 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

`x^2-4x+1 \implies a=1, \;\;b=-4, \;\;c=1`

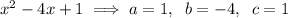
Therefore:

`\implies x=(-(-4) \pm √((-4)^2-4(1)(1)))/(2(1))`

`\implies x=(4 \pm 2√(3))/(2)`

`\implies x=2 \pm √(3)`

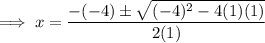
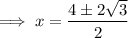
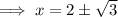
Therefore, the zeros of the given polynomial are:

• x = 6
• x = 2 + √3
• x = 2 - √3

Note: There are no complex zeros.