Question

Find the coordinates of B, C, and D given that AB=5 and BC = 10

Answer 1

B = (3, -5)

D = (0, -1)

C = (3, 5)

Explanation:

We want to find the coordinates of B, C, and D given that AB = 5 and BC = 10.

Because AB = 5 and BC = 10, we can find the slope of the line using the slope formula:

`\displaystyle \begin{aligned} m & = (\Delta y)/(\Delta x) \\ \\ & = ((10))/((5)) \\ \\ & = 2 \end{aligned}`

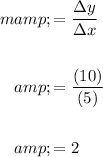
Point A(-2,-5) is on the line. Hence, the equation of the line is:

`\displaystyle \begin{aligned} y-y_1 &= m(x-x_1) \\ \\& = y-(-5) = 2(x-(-2)) \\ \\ y + 5 & = 2x+4 \\ \\ y & = 2x-1 \end{aligned}`

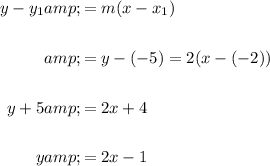
Because AB is 5, B is simply A shifted rightwards five units. Hence:

`\displaystyle B = (-2+5, -5) = (3, -5)`

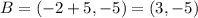
At Point D, x = 0. Hence:

`\displaystyle y = 2(0) -1 = -1`

Thus, D is at (0, -1).

B and C are collinear. Hence, the x value of C is 3:

`\displaystyle y = 3(2) - 1 = 5`

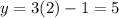
Therefore, C is at (3, 5).