Answer:
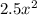
Explanation:
Let x be the shorter side of the rectangle, which is also its width (w), so:
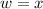
Given that the length of the rectangle is two-and-a-half times its width, this means the length (l) can be expressed as:
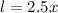
The area of a rectangle (A) is the product of its length (l) and width (w):
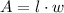
Substitute the expressions for length and width into the formula for area:
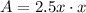
Simplify this expression:
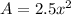
Therefore, the expression for the area of the rectangle in terms of x is:
