Answer:
(7, 8)
Explanation:
equation 1:
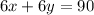
equation 2:

This system of equations can be solved for using the elimination method.
First, multiply both sides of the first equation by 3/2 to match the number of x's in both equations so that when we subtract the first equation from the second, the x's cancel and we can solve for y.
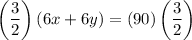
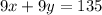
Next, subtract this from the second equation.
 ← eq. 2
← eq. 2
 ← modified eq. 1
← modified eq. 1
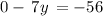
Then, solve for y by dividing by 7.
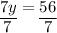
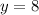
So, the y-coordinate of the solution pair is 8.
Now that we've solved for the y, all we have to do to get x is plug the solved y-value back into one of the equations. I'll use the first equation.
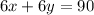
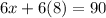
↓ multiplying out 6 and 8
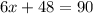
↓ subtracting 48 from both sides

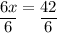
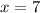
So, the x-coordinate of the solution pair is 7.
Finally, put the x- and y-coordinates together into an ordered pair in the form
 .
.
(7, 8)