Answer:
Assume that the two planets have the same radius. The escape velocity of planet a(with twice the mass) will be
 times the escape velocity of planet b.
times the escape velocity of planet b.
Step-by-step explanation:
Let
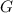 denote the gravitational constant.
denote the gravitational constant.
Consider a spherical planet of mass
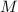 and radius
and radius
 . If an object of mass
. If an object of mass
 is on the surface of the planet, the gravitational potential energy
is on the surface of the planet, the gravitational potential energy
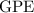 of that object will be:
of that object will be:
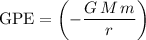 .
.
If this object is moving at a speed of
 , the kinetic energy
, the kinetic energy
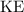 of this object will be
of this object will be
 .
.
If this object is moving at the escape velocity
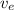 of the planet, the
of the planet, the
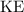 of this object will be equal to the opposite
of this object will be equal to the opposite
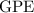 . In other words:
. In other words:
 .
.
Rearrange this equation to find escape velocity
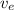 :
:
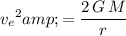 .
.
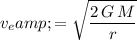 .
.
Assume that the radius
 of the planet is constant. Based on this equation, escape velocity
of the planet is constant. Based on this equation, escape velocity
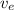 will be portional to
will be portional to
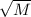 , the square root of the mass of the planet.
, the square root of the mass of the planet.
Hence, if the radius of planet a and planet b are equal, the escape velocity of planet a will be
 times the escape velocity of planet b.
times the escape velocity of planet b.