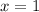Question

Please answer the complex system

Answer 1

`y = i`

`x = 1`

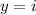
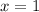
Explanation:

-------------------------------------------------------

Make
`x` the subject for
`ix-2y=-i` :

-------------------------------------------------------

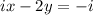Add 2y to both sides:

`\implies ix=-i+2y`

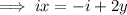
Divide both sides by i:

`\implies x=(-i+2y)/(i)`

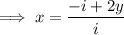
To remove i from the denominator, multiply the numerator and denominator by its complex conjugate:

`\implies x=(-i+2y)/(i) *(-i)/(-i)`

`\implies x=(i^2-2iy)/(-i^2)`

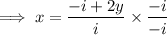
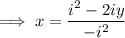
Apply the imaginary number rule
`i^2=-1` :

`\implies x=(-1-2iy)/(-(-1))`

`\implies x=(-1-2iy)/(1)`

`\implies x=-1-2iy`

-----------------------------------------------------------------------------------------------

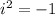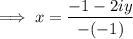
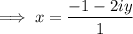
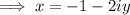
Substitute
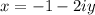`x=-1-2iy` into
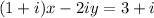`(1+i)x-2iy=3+i` and make y the subject:

-----------------------------------------------------------------------------------------------

`\implies (1+i)(-1-2iy)-2iy=3+i`

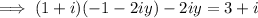
Apply complex arithmetic rule
`(a+bi)(c+di)=(ac-bd)+(ad+bc)i` :

`\implies (-1+2y)+(-2y-1)i-2iy=3+i`

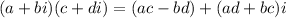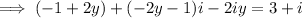
Simplify:

`\implies -1+2y-2iy-i-2iy=3+i`

`\implies 2y-4iy=4+2i`

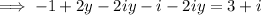
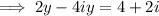
Factor:

`\implies 2(1-2i)y=2(2+i)`

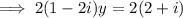
Divide both sides by
`2(1-2i)` :

`\implies (2(1-2i)y)/(2(1-2i))=(2(2+i))/(2(1-2i))`

`\implies y=((2+i))/((1-2i))`

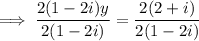
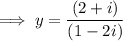
Multiply by the complex conjugate
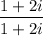`(1+2i)/(1+2i)` to remove
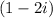`(1 - 2i)` from the denominator :

`\implies y=((2+i)(1+2i))/((1-2i)(1+2i))`

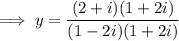
Apply complex arithmetic rule
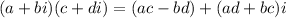`(a+bi)(c+di)=(ac-bd)+(ad+bc)i` to numerator:

`\implies y=((2-2)+(4+1)i)/((1-2i)(1+2i))`

`\implies y=(5i)/((1-2i)(1+2i))`

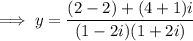
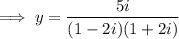
Apply complex arithmetic rule
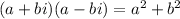`(a+bi)(a-bi)=a^2+b^2` to the denominator :

`\implies y=(5i)/(1^2+2^2)`

`\implies y=(5i)/(5)`

`\implies y=i`

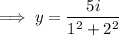
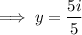
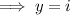
Therefore, one solution is
`y=i`

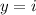
For the other solution, substitute
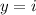`y=i` into
`x=-1-2iy`:

`\implies x=-1-2ii`

`\implies x=-1-2i^2`

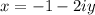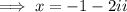
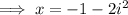
Apply the imaginary number rule
`i^2=-1` :

`\implies x=-1-2(-1)`

`\implies x=-1+2`

`\implies x=1`

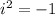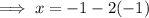
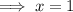
Therefore, the second solution is
`x = 1`