Question

A large tire contains 9.5 L of gas at a pressure

of 3.3 atm and a temperature of 279 K.
If the temperature of the gas increases to 303 K
and the volume is increased to 11.9 L,
what will be the new pressure of the gas?

Answer 1

new pressure = 2.86 atm

Step-by-step explanation:

To solve the given problem, we have to use the 'combined gas law', which is expressed in the formula:

`\boxed{(p_1V_1)/(T_1) = (p_2V_2)/(T_2)}`.

From the question, we know that the initial volume of the gas is 9.5 L, the initial pressure is 3.3 atm, and the initial temperature is 279 K. Therefore, V₁ = 9.5, p₁ = 3.3, and T₁ = 279.

We are also told that the gas temperature increases to 303 K and the volume increases to 11.9 L. Therefore, T₂ = 303 and V₂ = 11.9. We are then asked to calculate the new pressure (p₂).

To do this, we have to substitute the known values into the equation and solve it for p₂:

`{(p_1V_1)/(T_1) = (p_2V_2)/(T_2)}`

⇒
`(3.3 * 9.5)/(279) = (p_2 * 11.9)/(303)`

⇒
`303 * (3.3 * 9.5)/(279) = p_2 * 11.9`

⇒
`(3.3 * 9.5 * 303 )/(279 * 11.9) = p_2`

⇒
`p_2 = \bf 2.86 \ atm`

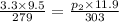
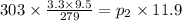
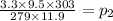
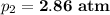
Therefore, the new pressure of the gas is 2.86 atm.