Question

What is the solution to the compound inequality in interval notation?

4(x +1) > -4 or 2x - 4 < -10

Answer 1

Answer:
`(-\infty, -3) \ \cup (-2, \infty)`

====================================================

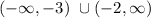
Step-by-step explanation:

Let's solve the first inequality.

4(x+1) > -4

4x+4 > -4

4x > -4-4

4x > -8

x > -8/4

x > -2

The inequality sign doesn't flip since we didn't divide both sides by a negative value.

Now let's solve the other inequality.

2x-4 < -10

2x < -10+4

2x < -6

x < -6/2

x < -3

-----------------------------------

To summarize:

• solving 4(x+1) > -4 leads to x > -2
• solving 2x-4 < -10 leads to x < -3

Draw out a number line. Place open holes at -3 and -2.

Shade to the right of -2 and to the left of -3 to indicate x > -2 and x < -3 respectively.

See the diagram below.

The interval in red is x < -3. This is the same as
`-\infty < \text{x} < -3` and that becomes the interval notation
`(-\infty, -3)`

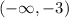
The interval in blue is x > -2. It is the same as
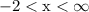`-2 < \text{x} < \infty` which becomes the interval notation
`(-2, \infty)`

Glue those interval notations together to end up with the final answer of
`(-\infty, -3) \ \cup (-2, \infty)`

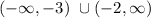
The "U" is the union symbol.