Answer:
The missing term in the output of the function
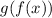 is -18.
is -18.
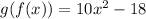
Explanation:
Function Composition
In mathematics, function composition is a term that encompasses a relationship between two functions wherein the output of one function is used as the input for another function. This relationship combines two functions to form a single function, known as a composite function. For future reference, function composition may also be denoted by a small circle, see below:
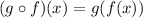
In the given problem, we must evaluate the composite function
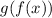 /
/
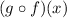 to identify the unknown term.
to identify the unknown term.
With composite functions, we begin evaluating from the inside. To evaluate
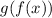 , we must substitute the output of the function
, we must substitute the output of the function
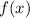 (given as the expression
(given as the expression
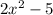 ) as the input (
) as the input (
 ) for the function
) for the function
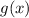 :
:
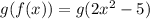
Now, using
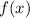 as the input (
as the input (
 ) for the function
) for the function
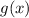 (given as the expression
(given as the expression
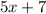 ), we can substitute
), we can substitute
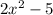 into the output for the function
into the output for the function
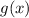 :
:
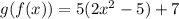
From here, we can go ahead and distribute the 5:
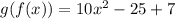
Combine like terms:
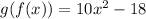
With the composite function evaluated, we can identify our missing term as
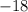 .
.