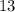Photo 1
Answer:
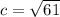
Explanation:
The pythagorean theorem is
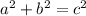
So if we plug in the other lengths it will be
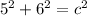
Now we have to find the value of

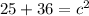
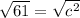
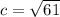
Photo 2
Answer:
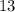
Explanation:
Use the distance formula;
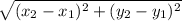
So if we plug in the other lengths it will be
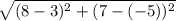
Then we simplify and get