Question

NO LINKS!! Please help me with these graphs. (NOT Multiple choice)

a. Show the end behavior
b. Shape the graph near the near x-intercepts.

1. p(x)= 2/3(3x - 6)(x + 2) (x - 3)^2

2. p(x) = (x - 3)^2 (x + 2) (2x + 7)^2

3. p(x) = (x - 5)(x + 2) (x - 1) - 30

Answer 1

`\begin{aligned}\textsf{1.} \quad \textsf{As}\;\; &x \rightarrow - \infty,\;\;f(x) \rightarrow + \infty\\ \textsf{As}\;\; &x \rightarrow +\infty,\;\;f(x) \rightarrow + \infty \end{aligned}`

`\begin{aligned}\textsf{2.} \quad \textsf{As}\;\; &x \rightarrow - \infty,\;\;f(x) \rightarrow - \infty\\ \textsf{As}\;\; &x \rightarrow +\infty,\;\;f(x) \rightarrow + \infty \end{aligned}`

`\begin{aligned}\textsf{3.} \quad \textsf{As}\;\; &x \rightarrow - \infty,\;\;f(x) \rightarrow - \infty\\ \textsf{As}\;\; &x \rightarrow +\infty,\;\;f(x) \rightarrow + \infty \end{aligned}`

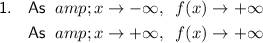
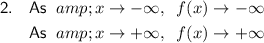
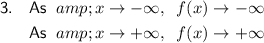
Explanation:

Root Multiplicity

Odd multiplicity → the graph will cross the x-axis at the root.

Even multiplicity → the graph will touch the x-axis at the root (but will not cross the x-axis).

Question 1

Given function:

`p(x)= (2)/(3)(3x - 6)(x + 2)(x - 3)^2`

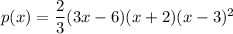
Therefore:

• Degree: 4 (even)
• Leading coefficient: positive

End behaviors:

`\textsf{As}\;\; x \rightarrow - \infty,\;\;f(x) \rightarrow + \infty`

`\textsf{As}\;\; x \rightarrow +\infty,\;\;f(x) \rightarrow + \infty`

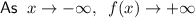
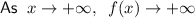
The x-intercepts of a function are when f(x)=0.

Therefore, the x-intercepts are:

• x = -2 with multiplicity 1
• x = 2 with multiplicity 1
• x = 3 with multiplicity 2

Therefore, the graph of the given function has 3 turning points.

• Begins in quadrant II
• Crosses the x-axis at x = -2
• Crosses the x-axis at x = 2
• Touches the x-axis at x = 3
• Ends in quadrant I

Question 2

Given function:

`p(x)=(x - 3)^2 (x + 2) (2x + 7)^2`

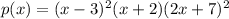
Therefore:

• Degree: 5 (odd)
• Leading coefficient: positive

End behaviors:

`\textsf{As}\;\; x \rightarrow - \infty,\;\;f(x) \rightarrow -\infty`

`\textsf{As}\;\; x \rightarrow +\infty,\;\;f(x) \rightarrow + \infty`

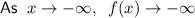
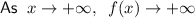
The x-intercepts of a function are when f(x)=0. Therefore, the x-intercepts are:

• x = -3.5 with multiplicity 2
• x = -1 with multiplicity 1
• x = 3 with multiplicity 2

Therefore, the graph of the given function has 4 turning points.

• Begins in quadrant III
• Touches the x-axis at x = -3.5
• Crosses the x-axis at x = -2
• Touches the x-axis at x = 3
• Ends in quadrant I

Question 3

Given function:

`p(x)=(x - 5)(x + 2)(x - 1)-30`

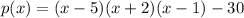
Therefore:

• Degree: 3 (odd)
• Leading coefficient: positive

End behaviors:

`\textsf{As}\;\; x \rightarrow - \infty,\;\;f(x) \rightarrow -\infty`

`\textsf{As}\;\; x \rightarrow +\infty,\;\;f(x) \rightarrow + \infty`

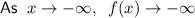
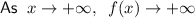
The graph has 2 turning points.

• Begins in quadrant III
• Turning points at x ≈ -0.7 and x ≈ 3.4
• Crosses the x-axis at x ≈ 5.8
• Ends in quadrant I