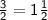Question

Solve for X - 18 points.

Answer 1

`\sf (3)/(2) = 1 (1)/(2) \\`

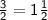
Explanation:

`\sf (1x)/(3) + (1)/(4) = (3)/(4) \\`

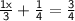
To solve easily, multiply the whole equation by it's LCM ( LCM of 3 & 4 is 12 ).

`\sf12 * ( \sf (1x)/(3) + (1)/(4) = (3)/(4) ) \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \ \\ \\ \sf (1x)/(3) * 12 + (1)/(4) * 12= (3)/(4) * 12\\ \\ \sf \sf (12x)/(3) + (12)/(4) = (36)/(4) \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ \\ \sf4x + 3 = 9 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:`

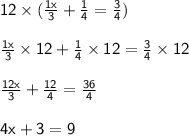
And now solve for x.

First, subtract 3 from both sides.

`\sf4x = 9 - 3 \\ \sf4x = 6`

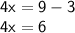
Divide both sides by 4.

`\sf \: x = (6)/(4) \\`

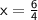
To write the fraction in its simplest form, divide both the numerator and denominator by 2.

`\sf (3)/(2) = 1 (1)/(2) \\`

Answer 2

x = 1 1/2

Explanation:

1/3 x + 1/4 = 3/4

Solving for x

Subtract 1/4 from each side

1/3 x + 1/4 -1/4 = 3/4-1/4

1/3 x = 2/4

Simplify

1/3x = 1/2

Multiply each side by 3

1/3 x * 3 = 1/2 * 3

x = 3/2

Changing to a mixed number

x = 1 1/2