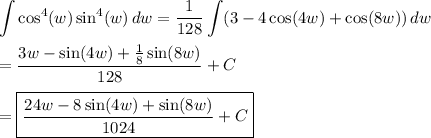Recall the double angle identity for sine:
sin(2x) = 2 sin(x) cos(x)
This means the given integrand is equivalent to
cos⁴(w) sin⁴(w) = (cos(w) sin(w))⁴ = (1/2 sin(2w))⁴ = 1/16 sin⁴(2w)
Also recall the half-angle identities for sine and cosine:
cos²(x) = 1/2 (1 + cos(2x))
sin²(x) = 1/2 (1 - cos(2x))
Then we can rewrite further as
1/16 sin⁴(2w) = 1/16 (sin²(2w))²
… = 1/16 (1/2 (1 - cos(4w)))²
… = 1/16 (1/4 (1 - 2 cos(4w) + cos²(4w))
… = 1/64 (1 - 2 cos(4w) + 1/2 (1 + cos(8w)))
… = 1/128 (3 - 4 cos(4w) + cos(8w))
You'll end up with the same solution as in the other answer: