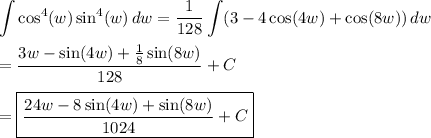Question

Hello everyone, I'm just having trouble on a question for my Calculus work. Does anyone know where to start with this problem? Any help would be greatly appreciated!

Answer 1

Recall the double angle identity for sine:

sin(2x) = 2 sin(x) cos(x)

This means the given integrand is equivalent to

cos⁴(w) sin⁴(w) = (cos(w) sin(w))⁴ = (1/2 sin(2w))⁴ = 1/16 sin⁴(2w)

Also recall the half-angle identities for sine and cosine:

cos²(x) = 1/2 (1 + cos(2x))

sin²(x) = 1/2 (1 - cos(2x))

Then we can rewrite further as

1/16 sin⁴(2w) = 1/16 (sin²(2w))²

… = 1/16 (1/2 (1 - cos(4w)))²

… = 1/16 (1/4 (1 - 2 cos(4w) + cos²(4w))

… = 1/64 (1 - 2 cos(4w) + 1/2 (1 + cos(8w)))

… = 1/128 (3 - 4 cos(4w) + cos(8w))

You'll end up with the same solution as in the other answer:

`\displaystyle \int \cos^4(w)\sin^4(w) \, dw = \frac1{128} \int (3 - 4\cos(4w) + \cos(8w)) \, dw \\\\ = (3w-\sin(4w)+\frac18\sin(8w))/(128) + C \\\\ = \boxed{(24w-8\sin(4w)+\sin(8w))/(1024) + C}`

Answer 2

sin(8w)/1024 -sin(4w)/128 +3w/128

Explanation:

No doubt there are a variety of formulas and identities that can be used. Absent knowledge of those, I found it convenient to rewrite the integrand using Euler's formula. It tells you ...

`\sin(x)=(e^(ix)-e^(-ix))/(2i),\quad\cos(x)=(e^(ix)+e^(-ix))/(2)`

After some only slightly messy algebra, we find ...

`\cos^4(w)\sin^4(w)=(\cos(8w)-4\cos(4w)+3)/(128)`

Then the integral becomes straightforward:

`\displaystyle \int{\cos^4(w)\sin^4(w)}\,dw=\int{(\cos(8w))/(128)}\,dw-\int{(\cos(4w))/(32)}\,dw+(3)/(128)\int{}\,dw\\\\=\boxed{(\sin(8w))/(1024)-(\sin(4w))/(128)+(3w)/(128)}`

__

Additional comment

The slightly messy algebra involves the identities ...

(a+b)(a-b) = a² -b²

(a -b)⁴ = a⁴ -4a³b +6a²b² -4ab³ +b⁴