Question

The vertex of a parabola is at (6,5), and its axis of symmetry is vertical. One of the x-intercepts is at (8, 0). What is the x-coordinate of the other x-intercept?

Answer 1

`x=4`

Explanation:

Vertex form of the quadratic equation:
`f(x) = a(x - h)^2+k`

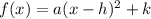
where the vertex is
`(h, k)`

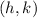
Given vertex = (6, 5):

`\implies f(x) = a(x - 6)^2+5`

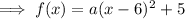
If one the x-intercepts is (8, 0):

`\implies f(8) =0`

`\implies a(8 - 6)^2+5=0`

`\implies 4a+5=0`

`\implies a=-(5)/(4)`

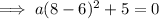
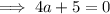
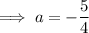
Therefore, equation of parabola:

`\implies f(x) = -\frac54(x - 6)^2+5`

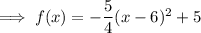
x-intercepts occur when f(x) = 0:

`\implies f(x)=0`

`\implies -\frac54(x - 6)^2+5=0`

`\implies -\frac54(x - 6)^2=-5`

`\implies (x - 6)^2=4`

`\implies x-6=\pm 2`

`\implies x=8, x=4`

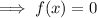
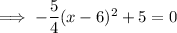
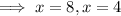
Therefore, the x-coordinate of the other x-intercept is 4.