2 Answers

Sakeena · Answer 1 · 2023-12-16T00:17:17+0000

Answer:

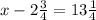
x-2 (3)/(4)=13 (1)/(4)

(where x is the original length of the pipe).

Original length of the pipe = 16 feet

Explanation:

Let x be the original length of the pipe.

Given a plumber cuts 2 3/4 feet from a pipe and now has a pipe that is 13 1/4 feet long, the equation that models this is:

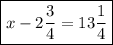
$\boxed{ x-2 (3)/(4)=13 (1)/(4)}$

To determine the length of the original pipe, solve the equation for x.

Add 2 3/4 to both sides of the equation:

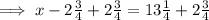
$\implies x-2 (3)/(4)+2 (3)/(4)=13 (1)/(4)}+2 (3)/(4)$

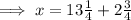
$\implies x=13 (1)/(4)}+2 (3)/(4)$

When adding mixed numbers, partition the mixed numbers into fractions and whole numbers, and add them separately:

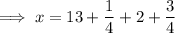
$\implies x=13 +(1)/(4)}+2 +(3)/(4)$

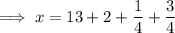
$\implies x=13 +2 +(1)/(4)}+(3)/(4)$

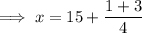
$\implies x=15 +(1+3)/(4)$

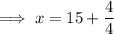
$\implies x=15 +(4)/(4)$

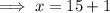
$\implies x=15 +1$

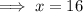
$\implies x=16$

Therefore, the original length of the pipe was 16 feet.

Please log in or register to add a comment.