Question

At sunset a tree casts a shadow 2.5 meters long. If the distance from the top of the tree to the farthest end of the shade is 4 meters, what is the height of the tree?​

Answer 1

It is as if it were a right triangle, where the shadow is one of its legs and the distance from the highest part of the tree to the farthest ends of the shadow is the hypotenuse, then we must find the other leg which would be the "height"

Where:

• S = Shadow
• H = Hypotenuse
• To = Height

Formula:

`\bold{ h^(2)= s^(2)+ a^(2)}`

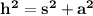
We solve:

`\bold{ a^(2)= h^(2)- s^(2)}`

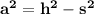
Once we have the formula, what we must do is find the Area of the tree, that is, that the tree is a right triangle, then:

`\bold{ a= \sqrt{ h^(2)- s^(2) }}`

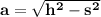
Now, we must take the square root in order to eliminate the square from the area.

`\bold{ a= \sqrt{ 4^(2)+ 2.5^(2) }}`

Once we did that, we put the Raised data that are 2.5 and 4 meters, to then add.

`\bold{a= √(16+6.25)}`

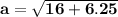
Next, once the data is added, they give us what is 16 and 6.25 now the next thing is to continue adding but this time it will be 16 and 6.25

`\bold{ a= √(22.25)}`

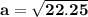
Now once we have the result of 22.25, the following will be that we will take the square root of 22.25

`\bold{ a=4.72m \:}`

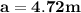
So once we have taken the square root it gives us 4.72

`\bold{{ \boxed{ \boxed{ \bold{ {Then=4.72m}}}} }}`

As we see, the result is 4.72 meters.