Question

I really need help with these 2 questions:

Rewrite the expression using rational exponents. (Simplify your answer completely.)
`√(x^3+y^3)`

Express the number in the form a/b, where a and b are integers.
27^{4/3}[/tex]

Answer 1

`\bullet\quad(x^3+y^3)^(1)/(2)\\\\\bullet\quad(81)/(1)`

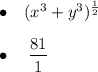
Explanation:

You want √(x³ +y³) written with a rational exponent, and 27^(4/3) written as a ratio of integers.

Root

The square root is the same as the 1/2 power. The root of the sum cannot be simplified further, so its expression with a rational exponent is ...

`√(x^3+y^3)=\boxed{(x^3+y^3)^(1)/(2)}`

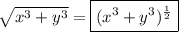
Power

The expression 27^(4/3) can be simplified to ...

`27^(4)/(3)=(\sqrt[3]{27})^4=3^4=81=\boxed{(81)/(1)}`

<95141404393>