Question

The first few terms of a geometric

sequence are given by 2, 4, 8, 16... What is
the value of the 28th term divided by the
26th term?

Answer 1

4

Explanation:

the nth term of a geometric sequence is

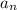`a_(n)` = a₁
`r^(n-1)`

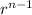
where a₁ is the first term and r the common ratio

here a₁ = 2 and r =
`(a_(2) )/(a_(1) )` =
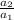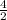`(4)/(2)` = 2

then

a₂₈ = 2
`(2)^(27)`

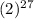
a₂₆ = 2
`(2)^(25)`

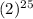
using the rule of exponents

`(a^(m) )/(a^(n) )` =
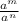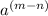`a^((m-n))` , then

`(a_(28) )/(a_(26) )`

=
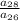
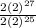`(2(2)^(27) )/(2(2)^(25) )` ( cancel 2 on numerator/ denominator )

=
`(2^(27) )/(2^(25) )`

=
`2^((27-25))`

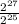
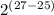
= 2²

= 4