Answer:
4
Explanation:
the nth term of a geometric sequence is
 = a₁
= a₁
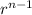
where a₁ is the first term and r the common ratio
here a₁ = 2 and r =
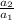 =
=
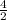 = 2
= 2
then
a₂₈ = 2
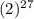
a₂₆ = 2

using the rule of exponents
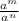 =
=
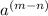 , then
, then

=
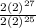 ( cancel 2 on numerator/ denominator )
( cancel 2 on numerator/ denominator )
=
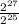
=
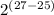
= 2²
= 4