Answer:
The speed of the bodies will be 2.27 m/s
Step-by-step explanation:
The picture bellow is the solution of the task, but I will give additional clarification here in case that the steps are not clear enough.
First, we want to calculate the acceleration of the whole system. To do that, we'll need to divide the net force (total force) by total mass. In my diagram, I've drawn all the forces which act on the body, but only those forces which I've circled in blue are relevant since all the other forces cancel each other out. The relevant forces are: force due to gravitational acceleration (g) on m2, component of the force due to g acting in the direction parallel to the plane, and the force of friction which always opposes the motion (aka acts in the opposite direction from the direction in which the body is moving; in this case down the plane). Since m2 pulls m1 up the plane, that will be our positive direction, so m2*g will be positive and other two forces will be negative. Putting all the data into the formula, we get the acceleration a ≈ 4.36 m/s².
Next step is calculating the time m2 takes to reach the ground. We use formula:
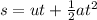 ut will be 0 since the system was initially at rest. When we rearange the formula and put in the values we get that the time t ≈ 0.52 s.
ut will be 0 since the system was initially at rest. When we rearange the formula and put in the values we get that the time t ≈ 0.52 s.
Finally, we get the velocity by multiplying time taken to reach the ground by the acceleration of the system.