Answer:
4500
Explanation:
This can be solved in more than one way. One method is to use permutations and see which digits can appear how many times in which position in the possible list of even numbers between 1000 and 9999
However, I think approaching this from an arithmetic progression perspective is easier to explain.
An arithmetic progression or sequence is a sequence of numbers such that there is a common difference between consecutive numbers.
For example, 2, 4, 6, 8, 10... is an arithmetic sequence with a common difference.
Given the first term in the sequence, we can find the nth term using the formula:
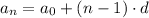
where
 is the nth term,
is the nth term,
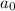 is the first term
is the first term
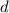 is the common difference
is the common difference
Treating the even numbers from 1000 to 9999 as an arithmetic sequence, we get the following:

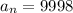 (since the last number has to be even
(since the last number has to be even
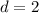
Let
 be the number of possible values
be the number of possible values
Plug this into the formula and solve for

9998 = 1000 + (n-1)2
9998 = 1000 + 2n - 2
9998 = 998 + 2n
9998-998 = 2n
9000 = 2n
Switch sides:
2n = 9000
Divide by 2 to get
n = 9000/2 or
n = 4500