Question

How many 4-digit numbers can be formed if the number must be divisible by 2 and digits can be repeated?

Answer 1

4500

Explanation:

This can be solved in more than one way. One method is to use permutations and see which digits can appear how many times in which position in the possible list of even numbers between 1000 and 9999

However, I think approaching this from an arithmetic progression perspective is easier to explain.

An arithmetic progression or sequence is a sequence of numbers such that there is a common difference between consecutive numbers.

For example, 2, 4, 6, 8, 10... is an arithmetic sequence with a common difference.

Given the first term in the sequence, we can find the nth term using the formula:

`a_n = a_0 + (n-1)\cdot d`

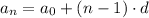
where

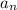`a_n` is the nth term,

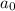`a_0` is the first term

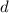`d` is the common difference

Treating the even numbers from 1000 to 9999 as an arithmetic sequence, we get the following:

`a_0 = 1000`

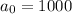
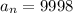`a_n = 9998` (since the last number has to be even

`d = 2`

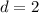
Let
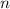`n` be the number of possible values

Plug this into the formula and solve for
`n`

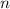
9998 = 1000 + (n-1)2
9998 = 1000 + 2n - 2

9998 = 998 + 2n
9998-998 = 2n
9000 = 2n

Switch sides:

2n = 9000

Divide by 2 to get
n = 9000/2 or

n = 4500