Answer:
- Domain: real numbers except {-4, -3, 0}
- Range: real numbers except {2}
- Intercepts: (-1, 0); no y-intercept (see Holes)
- Asymptotes: horizontal, y = 2; vertical, x = -3
- Holes: (-4, 6), (0, 2/3)
Explanation:
You want the domain, range, intercepts, asymptotes, and holes of the rational function f(x) = (2x³ +10x² +8x)/(x³ +7x² +12).
Simplified
The given function can be simplified by cancelling common factors from numerator and denominator. These cancelled factors show where the holes are in the graph.
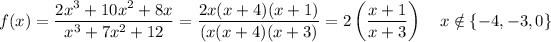
Domain
The function is defined for all real numbers except those where the denominator is zero: {-4, -3, 0}.
Range
The function can produce every output value except the value of the horizontal asymptote: y = 2. The range is all real numbers except 2.
Intercepts
The x-intercept is found where the numerator of the simplified function is zero: x = -1
The y-intercept is the function value at x=0. The function is undefined there, so the y-intercept does not exist. (The limit as x approaches zero is y = 2/3.)
Asymptotes
The function has a horizontal asymptote at the y-value corresponding to the ratio of the highest-degree terms of the numerator and denominator: y = 2.
The vertical asymptote is at the uncanceled denominator zero, x = -3.
Holes
The holes are where a numerator and denominator factor cancel. The y-value at the hole is the limit of the function value as x approaches the hole location. This is the value of the simplified function.
The holes are (-4, 6) and (0, 2/3).