Answer:
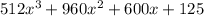
Step-by-step explanation: Start by spreading the expression out so it turns into (8x + 5)*(8x + 5)*(8x + 5). (* means multiply). Then, foil (multiply the first numbers, outside numbers, inside numbers, and last numbers to form a new expression) the first two expressions to get 64x^2+80x+25*(8x + 5). Foil that again, going through and multiplying each number from both expressions by every number in the other expression to get 512x^3+960x^2+600x+125. Hope that helps.