Answer:
Amplitude = 3
Period = π
Explanation:

Given function:
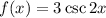
Therefore:
Period
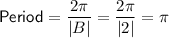
Amplitude
The amplitude of the given function is 3, so:
- minimum points are when y = 3.
- maximum points are when y = -3.
x-values of minimum points
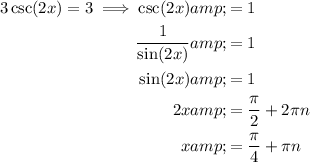
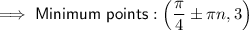
x-values of maximum points
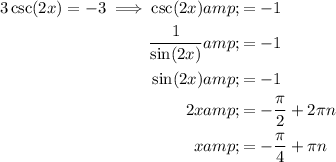
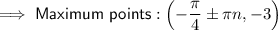
Asymptotes:
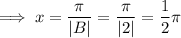
Therefore, there are vertical asymptotes every ¹/₂π.
To graph the given function:
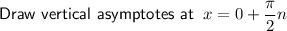
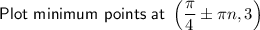
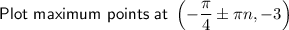
- Draw curves between the asymptotes with the given min/max points.