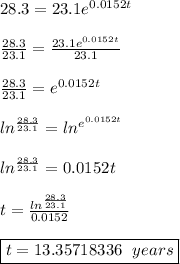Answer: 23.1, 13.35718336 years or 14 rounded
Explanation:
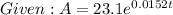
when A = end amount, and t = years after 2000
Part A).
What was the population of the state in 2000. According to our function, this would be when t = 0
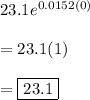
Part B).
When will the population of the state reach 28.3 million?
This would be when A = 28.3