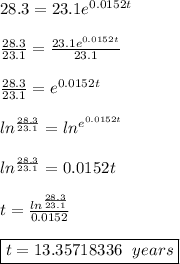Question

help meeeeeeeeeeeeeeee pleaseeeeeeehelp meeeeeeeeeeeeeeee pleaseeeeeeehelp meeeeeeeeeeeeeeee pleaseeeeeeehelp meeeeeeeeeeeeeeee pleaseeeeeeehelp meeeeeeeeeeeeeeee pleaseeeeeeehelp meeeeeeeeeeeeeeee pleaseeeeeee

Answer 1

Answer: 23.1, 13.35718336 years or 14 rounded

Explanation:

`Given:A= 23.1e^(0.0152t)`

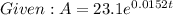
when A = end amount, and t = years after 2000

Part A).

What was the population of the state in 2000. According to our function, this would be when t = 0

`23.1e^(0.0152(0))\\\\=23.1(1)\\\\=\boxed{23.1}`

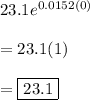
Part B).

When will the population of the state reach 28.3 million?

This would be when A = 28.3

`28.3=23.1e^(0.0152t)\\\\(28.3)/(23.1) =(23.1e^(0.0152t))/(23.1) \\\\(28.3)/(23.1) =e^(0.0152t)\\\\ln^{(28.3)/(23.1) }=ln^{e^(0.0152t)}\\\\ln^{(28.3)/(23.1) }=0.0152t\\\\t=\frac{ln^{(28.3)/(23.1) }}{0.0152} \\\\\boxed{t=13.35718336 \ \ years}`