Question

Slope of line that passes through (2,7) and (-4,19)

Answer 1

To calculate the slope of the line, we have that its points are A(x₁, y₁) and B(x₂,y₂), we apply the following formula:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{m=(\Delta y)/(\Delta x) \iff m=(y_2-y_1)/(x_2-x_1) } \end{gathered}$}}`

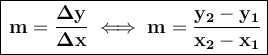
To solve, we have that the points are:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{A(x_1=\underbrace{2} \ \ , \ \ y_1=\overbrace{7} \ ) \ and \ B(x_2=\underbrace{-4} \ \ , \ \ y_2=\overbrace{19} } \end{gathered}$}}`

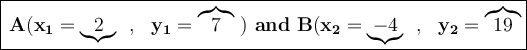
What we do to solve is that we substitute this data in the formula provided above.

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{m=(y_2-y_1)/(x_2-x_1) } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{m=(19-7)/(-4-2) } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{m=(12)/(-6)=-2 } \end{gathered}$}}`

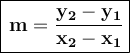
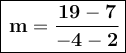
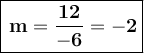
The slope of the line that passes through (2,7) and (-4,19) is -2.