Answer:
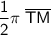
Explanation:
The angle at the circumference in a semicircle is a right angle.
Therefore, as
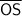 is the diameter of circle T, and point Q is on the circumference of the circle:
is the diameter of circle T, and point Q is on the circumference of the circle:
Therefore, if m∠MTN = m∠SQO then:
Angles around a point sum to 360°.
As 90° is one quarter of 360°, the measure of arc MN is one quarter of the circumference of circle T.
The circumference of a circle is 2πr, where r is the radius.
Therefore:
