Consider the sequence: 6, 10, 14, 18, 22,. . . . For this sequence, what is a3? a3 =.

Question

asked Apr 10, 2023 199k views

1 Answer

Faesal · Answer 1 · 2023-04-16T03:16:30+0000

Answer:

14

Explanation:

A sequence is given to us , which is ;

$\longrightarrow 6,10,14,18,22$

We need to find out the third term of the sequence . The third term is 14 which is itself given in the question . We can also find it as ,

The given sequence is in Arithmetic progression since a common number is added to get the next term of the sequence .

Firstly let's find out the common difference . For this we can subtract any two consecutive terms . So ,

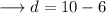
$\longrightarrow d = 10 -6\\$

$\longrightarrow d =4$

Now we know that the general term of the sequence in an AP is given by ,

$\longrightarrow T_n = a + (n-1)d$

The first term is 6 and common difference is 4 . On substituting the respective values ,

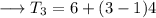
$\longrightarrow T_3 = 6 + (3-1)4\\$

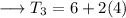
$\longrightarrow T_3 = 6 + 2(4)\\$

$\longrightarrow T_3 = 6 +8\\$

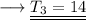
$\longrightarrow \underline{\underline{T_3=14}}$

This is the required answer!