Answer:
See attachment.
Explanation:
Given function:
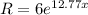
Given parameters:
- Domain: [0, 0.3]
- Range: [0, 100]
The y-intercept is when x = 0:
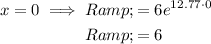
Locate more points on the curve by inputting different values of x from the given domain:

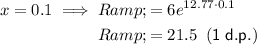
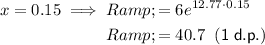
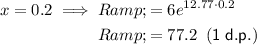
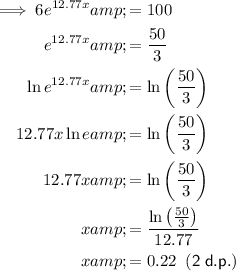
Find the x-value when R = 100:
To draw the graph:
- Use a scale of x : y = 1 : 400.
- Plot the y-intercept at (0, 6).
- Plot points (0.05, 11.4), (0.1, 21.5), (0.15, 40.7), (0.2, 77.2).
- Plot point (0.22, 100).
- Draw a curve through the points.