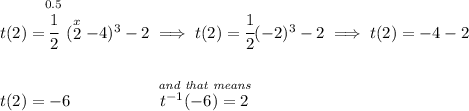well, we could just find the inverse of t(x) and then plug in the "2" and get it.
OR
we can just recall that "the inverse of t(x) has a domain that's the same as the range of t(x)"
what the heck all that means?
well, it means that for any (a , b) pair in t(x), the inverse t⁻¹(x) has an exact pair but sideways, namely (b , a).
so, if we want t⁻¹( x ) = 2, that means that t⁻¹( a ) has a pair of ( a , 2 ), well, hell, that also means that t(x) has a pair that ( 2 , a ).
so, if we want to know what "a" is, let's just find f(2), because since t⁻¹( a ) = 2, then t( 2 ) = a :)