Question

Simplify

(Look at the picture)
No links please

Answer 1

`\frac{\sqrt[4]{3}}{ \sqrt[5]{3} } = \frac{ {3}^{ (1)/(4) } }{ {3}^{ (1)/(5) } } \\ = {3}^{ (1)/(4) - (1)/(5) } \\ = {3}^{ (5)/(20) - (4)/(20) } \\ = {3}^{ (1)/(20) } \: or \: \sqrt[20]{3}`

Answer 2

`\sqrt[20]{3}`

Explanation:

Using the radical rule (
`\sqrt[x]{a}=a^{(1)/(x)`), we can rewrite the fraction:

(3^1/4)/(3^1/5)

Since we are dividing exponents with the same base, we can subtract the two exponents to get:

3^(1/4-1/5)

Convert both fractions to a base of 20:

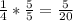`(1)/(4)*(5)/(5)=(5)/(20)` (notice we can only multiply by a number of itself since it is essentially like multiplying the fraction by 1)

`(1)/(5)*(4)/(4)=(4)/(20)`

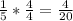
Therefore we have:

3^(5/20-4/20)=3^(1/20)

Which again using the radical rule we can rewrite as:

`\sqrt[20]{3}`