Answer:
y =
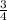 (x - 2)² - 5
(x - 2)² - 5
Explanation:
the equation of a parabola in vertex form is
y = a(x - h)² + k
where (h, k ) are the coordinates of the vertex and a is a multiplier
here (h, k ) = (2, - 5 ) , then
y = a(x - 2)² - 5
to find a substitute (- 2, 7 ) into the equation
7 = a(- 2 - 2)² - 5 ( add 5 to both sides )
12 = a(- 4)² = 16a ( divide both sides by 16 )
 = a , that is a =
= a , that is a =
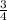
y =
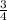 (x - 2)² - 5 ← equation in vertex form
(x - 2)² - 5 ← equation in vertex form