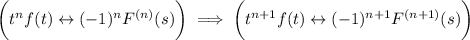Let k = 1, for a start. By definition of the Laplace transform,
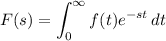
Differentiate both sides with respect to s :
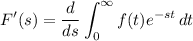
![\displaystyle F'(s) = \int_0^\infty (\partial)/(\partial s) \left[f(t) e^(-st)\right] \, dt](https://img.qammunity.org/2023/formulas/mathematics/college/pvvqu0qe669vqcb3bvmuoil86uhw6xiyc7.png)

so that
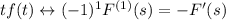 is indeed true.
is indeed true.
Suppose the claim is true for arbitrary integer k = n, which is to say that
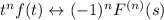 . Then if k = n + 1, we have
. Then if k = n + 1, we have
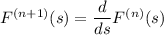
Consider the two cases:
• If k = n + 1 is even, then n is odd, so
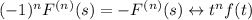
and it follows that
![F^((n+1))(s) = \displaystyle (d)/(ds) \left[-\int_0^\infty t^n f(t) e^(-st) \, dt \right]](https://img.qammunity.org/2023/formulas/mathematics/college/yy20xuj5u0uusim9ifw1vp3qz61svy1uwy.png)
![F^((n+1))(s) = \displaystyle -\int_0^\infty (\partial)/(\partial s)\left[ t^n f(t) e^(-st) \right] \, dt](https://img.qammunity.org/2023/formulas/mathematics/college/u3mi4eiossw6ar2142zpo6vqxtrgdz3knv.png)
![F^((n+1))(s) = \displaystyle (d)/(ds) \left[-\int_0^\infty t^n f(t) e^(-st) \, dt \right]](https://img.qammunity.org/2023/formulas/mathematics/college/yy20xuj5u0uusim9ifw1vp3qz61svy1uwy.png)


• Otherwise, if k = n + 1 is odd, then n is even, so
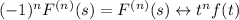
The rest of the proof is the same as the previous case.
So we've proved the claim by induction:
•
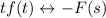 , and
, and
•