Question

NO LINKS!! Use tests for symmetry to determine which graphs from the list below are symmetric with respect to the y-axis, the x-axis, and the origin. (Select all that apply.) Part 1​

Answer 1

`\begin{aligned}\textsf{(a)} \quad y&=-6x^2\\y&=4x^2-2\end{aligned}`

`\textsf{(b)} \quad x=(1)/(4)y^2`

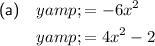
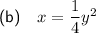
Explanation:

Part (a)

A graph is symmetric with respect to the y-axis if for every point (a, b) on the graph, there is also a point (-a, b) on the graph.

Linear functions are not symmetric with respect to the y-axis.

Quadratic functions are symmetric with respect to the y-axis if the y-axis is their axis of symmetry, so when the variable x is squared.

Cubic functions are not symmetric about the y-axis.

Square root functions are not symmetric about the y-axis.

There are two quadratic functions with x² in the given answer options.

Test to see if they are symmetric with respect to the y-axis.

Test for symmetry

To determine if a graph is symmetric with respect to the y-axis, replace all the x's with (−x). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the y-axis.

Given function:

`y=-6x^2`

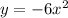
Replace x with (-x):

`\implies y=-6(-x)^2`

`\implies y=-6x^2`

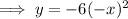
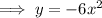
Therefore, as the function is equal to the original function, this function is symmetric with respect to the y-axis.

Given function:

`y=4x^2-2`

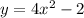
Replace y with (-y) and x with (-x):

`\implies y=4(-x)^2-2`

`\implies y=4x^2-2`

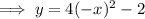
Therefore, as the function is equal to the original function, this function is symmetric with respect to the y-axis.

Part (b)

A graph is symmetric with respect to the x-axis if for every point (a, b) on the graph, there is also a point (a, -b) on the graph.

Linear functions are not symmetric with respect to the x-axis.

Quadratic functions are symmetric with respect to the x-axis if the x-axis is their axis of symmetry, so when the variable y is squared.

Cubic functions are not symmetric about the x-axis.

Square root functions are not symmetric about the x-axis.

There is one quadratic functions with y² in the given answer options.

Test to see if it is symmetric with respect to the x-axis.

Test for symmetry

To determine if a graph is symmetric with respect to the x-axis, replace all the y's with (−y). If the resultant expression is equivalent to the original expression, the graph is symmetric with respect to the x-axis.

Given function:

`x=(1)/(4)y^2`

Replace y with (-y):

`\implies x=(1)/(4)(-y)^2`

`\implies x=(1)/(4)y^2`

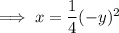
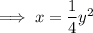
Therefore, as the function is equal to the original function, this function is symmetric with respect to the x-axis.