Question

A 4,155 kg car moving at 28.3 m/s hits a stationary truck with a mass of 3,172 kg. If the two vehicles become stuck together in the collision, how fast do they move away from the point of impact?

Answer 1

Approximately
`16.0\; {\rm m\cdot s^(-1)}`.

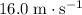Step-by-step explanation:

When an object of mass
`m` travels at a velocity of
`v`, the momentum
`p` of that object will be
`p = m\, v`.

In this example, the momentum of the car before the collision will be:

`\begin{aligned}p &= m\, v \\ &= (4155\; {\rm kg})\, (28.3\; {\rm m\cdot s^(-1)}) \\ &\approx 1.17587* 10^(5)\; {\rm kg \cdot m\cdot s^(-1)} \end{aligned}`.

Since the truck was initially not moving, the initial momentum of the truck will be
`(3172\; {\rm kg})\, (0\; {\rm m\cdot s^(-1)}) = 0\; {\rm kg \cdot m\cdot s^(-1)}`.

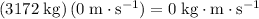Momentum is conserved in collisions. In other words, the sum of the momentum of the truck and the car will be the same right before and after the collision.

The sum of the momentum of the truck and the car was approximately
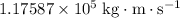`1.17587* 10^(5)\; {\rm kg \cdot m\cdot s^(-1)}` right before the collision. By the conservation of momentum, the sum of the momentum of the two vehicles right after the collision will also be
`1.17587* 10^(5)\; {\rm kg \cdot m\cdot s^(-1)}\!`.

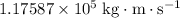The velocity of the two vehicles right after the collision will be the same since the vehicles are stuck together. Let
`v` denote this velocity.

The sum of the mass of the two vehicles is
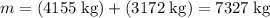`m = (4155\; {\rm kg}) + (3172\; {\rm kg}) = 7327\; {\rm kg}`. Divide the total momentum of the two vehicles by their total mass to find the velocity:

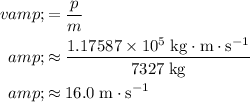`\begin{aligned}v &= (p)/(m) \\ &\approx \frac{1.17587* 10^(5)\; {\rm kg \cdot m\cdot s^(-1)}}{7327\; {\rm kg}} \\ &\approx 16.0\; {\rm m\cdot s^(-1)}\end{aligned}`.