Answer:
The value of x is 34.
Step-by-step explanation:
QUESTION :
Find x:
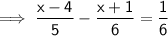

CONCEPT :
Here, we will use the below following steps to find a solution using the transposition method:
- Step 1 :- we will Identify the variables and constants in the given simple equation.
- Step 2 :- then we Simplify the equation in LHS and RHS.
- Step 3 :- Transpose or shift the term on the other side to solve the equation further simplest.
- Step 4 :- Simplify the equation using arithmetic operation as required that is mentioned in rule 1 or rule 2 of linear equations.
- Step 5 :- Then the result will be the solution for the given linear equation.

SOLUTION :
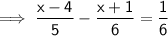
Taking LCM of both denominators.
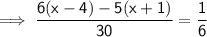
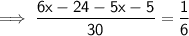
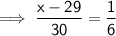
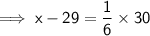

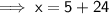
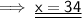
Hence, the value of x is 34.

Verification :
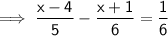
Substituting the value of x in the equation :
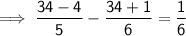
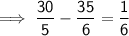
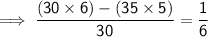
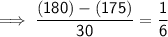
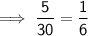

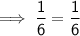

Hence verified!
————————————————