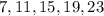Answer:
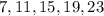
Explanation:
Let the 5 Numbers be:
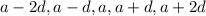
The sum of these 5 numbers are:
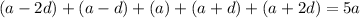
Given in the statement, we now have
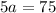
⇒

The product of the greatest and the least numbers of the series
=
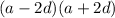
=
 -
-
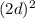
=
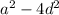
By the statement
=
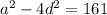
Substituting

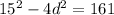
⇒
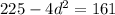
⇒
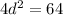
⇒
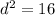
⇒
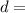 ±
±

Now, taking both
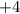 and
and
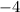 we get the following:
we get the following: