Question

Write an exponential function represented by the graph
y= ?

Answer 1

The exponential function is:
`\(y = 8 \cdot \left((1)/(2)\right)^x\)`

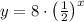
The general form of an exponential function is
`\(y = a \cdot b^x\)`, where a is the initial value or the value of y when x = 0, b is the base of the exponential function, and x is the exponent.

Given the points (0,8), (1,4), (2,2), and (3,1), let's determine the values of a and b in the exponential function.

Using the Point (0,8):

When x = 0, y = 8. This gives us the initial value, a = 8.

Using the Point (1,4):

Substituting x = 1 and y = 4 into the exponential function:

`\[4 = 8 \cdot b^1\]`

`\[b = (4)/(8) = (1)/(2)\]`

Therefore, the exponential function represented by the given graph is:

`\[y = 8 \cdot \left((1)/(2)\right)^x\]`

Answer 2

y = 8
`((1)/(2)) ^(x)`

Explanation:

an exponential function can be expressed in the form

y = a
`b^(x)`

to find a and b use points that lie on the graph

using (0, 8 ) , then

8 = a
`b^(0)` [
`b^(0)` = 1 ] , then a = 8

y = 8
`b^(x)`

using (1, 4 ) , then

4 = 8
`b^(1)` = 8b ( divide both sides by 8 )

`(4)/(8)` = b , that is b =
`(1)/(2)`

y = 8
`((1)/(2)) ^(x)` is the exponential function