The exponential function is:
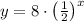
The general form of an exponential function is
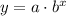 , where a is the initial value or the value of y when x = 0, b is the base of the exponential function, and x is the exponent.
, where a is the initial value or the value of y when x = 0, b is the base of the exponential function, and x is the exponent.
Given the points (0,8), (1,4), (2,2), and (3,1), let's determine the values of a and b in the exponential function.
Using the Point (0,8):
When x = 0, y = 8. This gives us the initial value, a = 8.
Using the Point (1,4):
Substituting x = 1 and y = 4 into the exponential function:
![\[4 = 8 \cdot b^1\]](https://img.qammunity.org/2023/formulas/mathematics/college/dy55ckmb2fkrlfv5cd0qwemc98tlyvlizi.png)
![\[b = (4)/(8) = (1)/(2)\]](https://img.qammunity.org/2023/formulas/mathematics/college/3ccazb0qa9ytk30pnnmxligg4804on0onp.png)
Therefore, the exponential function represented by the given graph is:
![\[y = 8 \cdot \left((1)/(2)\right)^x\]](https://img.qammunity.org/2023/formulas/mathematics/college/vk8hixldk0uzszny3in1b8n1983e49b6ji.png)