Question

For each of the following equations, solve for the variable.

Answer 1

1.
`z =- (10)/(17)`

2.
`y = -(8)/(53)`

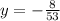
Explanation:

Pre-Solving

We are given the equations
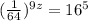`((1)/(64))^(9z) = 16^5` and
`36 ^ {(7y+4) = ((1)/(216) )^(13y)`.

We want to solve for the variables in both of them.

Solving

No. 1:

The first one is
`((1)/(64) ) ^ {9z} = 16^5`

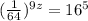
Remember that for exponential equations, we want to arrive at the same base.

We can simplify the equations to help us arrive at a same base.

First for
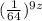`((1)/(64)) ^ {9z}`, recall that if we have
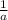`(1)/(a)`, that is equal to
`a ^( -1)`.

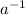This means that
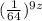`((1)/(64)) ^ {9z}` will be
`(64^(-1)) ^ {9z}`

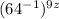
Remember that also if we have
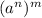`(a^n)^m`, that is equal to
`a^(nm)`.

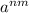So this means that
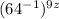`(64^(-1)) ^ {9z}` is equal to
`64^(-9z)`

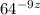
Notice how 64 is
`2^6`.

This means that we can simplify the base of 64 to become:
`(2^6)^(-9z)`, which can then be further simplified to
`2^(-54z)`.

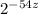Now, for the right side, recall that 16 is
`2^4`.

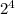We can rewrite
`16^5` to be
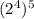`(2^4)^5`, which will be
`2^(20)`.

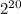Now, our equation is:

`2^(-54z) = 2^(20)`

Since we have arrived at the same base, we can take the exponents and set them equal to each other.

-54z = 20

Divide both sides by -54.

z = -20/54

Simplify

z = -10/27

No. 2:

We have:
`36 ^ {(7y+4) = ((1)/(216) ) ^ {13y}`

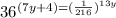
Let's start with the left side.

36 can be simplified to 6².

We can rewrite
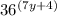`36 ^ {(7y+4)` as
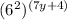`(6^2)^{(7y+4)`, which simplifies to
`6^{2(7y+4)`.

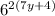For the right side, we can first simplify
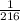`(1)/(216)` to
`216^(-1)`

We now have:
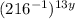`(216^(-1))^(13y)`, which is
`216 ^ {-13y}`.

216 is actually 6³, so
`216 ^ {-13y}` can be rewritten as
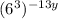`(6^3) ^ {-13y}`, which simplifies to
`6^(-39y)`.

We now have:

`6^{2(7y+4) = 6^(-39y)`

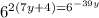
Since the bases are the same, we can take the exponents and set them equal to each other.

2(7y+4) = -39y

Multiply.

14y + 8 = -39y

Subtract 14y to both sides.

8 = -53y

Divide both sides by -53.

-8/53 = y