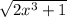Question

By using the Chain Rule, differentiate with respect to x:

Answer 1

y'=9x^2 *
`√(2x^3 + 1)`

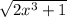
Explanation:

y=(4x^3 - 2x^3 + 1)^3/2 ==>
`√(?)`=?^1/2

y'=3/2(4x^3 - 2x^3 + 1)^1/2 * (4x^3 - 2x^3 + 1)'

y'=3/2(2x^3 + 1)^1/2 * (12x^2 - 6x^2 + 0)

y'=3/2(2x^3 + 1)^1/2 * (12x^2 - 6x^2 + 0)

y'=3/2(2x^3 + 1)^1/2 * 6x^2

y'=3/2 *
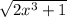`√(2x^3 + 1)` * 6x^2

y'=3/2 * 6x^2 *
`√(2x^3 + 1)`

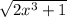
y'=3 * 6x^2/2 *
`√(2x^3 + 1)`

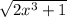
y'=3 * 3x^2 *
`√(2x^3 + 1)`

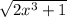
y'=9x^2 *
`√(2x^3 + 1)`