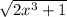Answer:
y'=9x^2 *
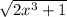
Explanation:
y=(4x^3 - 2x^3 + 1)^3/2 ==>
 =?^1/2
=?^1/2
y'=3/2(4x^3 - 2x^3 + 1)^1/2 * (4x^3 - 2x^3 + 1)'
y'=3/2(2x^3 + 1)^1/2 * (12x^2 - 6x^2 + 0)
y'=3/2(2x^3 + 1)^1/2 * (12x^2 - 6x^2 + 0)
y'=3/2(2x^3 + 1)^1/2 * 6x^2
y'=3/2 *
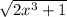 * 6x^2
* 6x^2
y'=3/2 * 6x^2 *
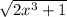
y'=3 * 6x^2/2 *
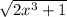
y'=3 * 3x^2 *
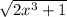
y'=9x^2 *