Answer:
7.39466667 (8 d.p.)
Explanation:
We can approximate the value of eˣ for any x using the following sum formula:
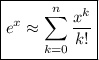
To approximate
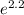 with n = 3, substitute x = 2.2 and n = 3 into the given sum formula:
with n = 3, substitute x = 2.2 and n = 3 into the given sum formula:
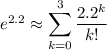
To calculate the sum, substitute k with each value from 0 to 3 and add the results together:

Therefore, the approximate value of
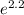 is:
is:
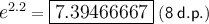
Note: To obtain a more accurate approximate value, increase the value of n.