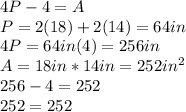Answer:
Explanation:
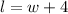



Since w represents a measurement of a physical object in inches, it cannot be negative. So,
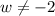 . The width of the rectangle is 14 inches.
. The width of the rectangle is 14 inches.
The length is given as 4 inches more than the width, so the length is 18 inches.
This satisfies all the requirements of the question: